Невизначені та визначені інтеграли. Методи інтегрування

Інтегралом є числове значення, яке дорівнює площі під графіком у вигляді функції з певним інтервалом (визначений) або нової функції, похідною якої виступає вихідна функція (невизначений). Ці два значення пов’язані тим, що визначений інтеграл будь-якої функції, яка може бути інтегрована, можна знайти, використовуючи невизначений інтеграл і результат основної теореми числення. 

Процес знаходження невизначеного інтеграла має назву інтегрування. За допомогою інтегрування можна визначати об’єм, роботу, відстань, швидкість, прискорення, кінетичну енергію, середнє значення функції, центр мас, площу поверхні, довжину дуги, ймовірність тощо. 

Розглянемо основні властивості визначеного інтеграла:

Що таке табличні інтеграли?

Таблична інтеграція – спеціальний метод інтегрування за частинами. Його можна застосовувати до певних функцій типу f(x)=g(x)h(x), у якій одна із функцій g(x) або h(x) може бути легко диференційована декілька разів, в той час як друга може бути так само просто інтегрована кілька разів. Взагалі розрізняють два типи табличної інтеграції: 1) коли один із факторів f(x) багаторазового диференціювання переходить в 0; 2) коли жоден із факторів багаторазової диференціації не переходить в 0.

Нижче подана таблиця з 11 інтегралів функцій, яка була складена на основі таблиці похідних. 

Розглянемо замітки до прикладу №4. Якщо х<0, це означає, що ln |x| = ln (-x).

Як застосовувати метод заміни змінної в інтегруванні?

Для початку треба володіти методом заміни змінної у невизначеному інтегралі. Маємо визначений інтеграл від а до b f(x)dx. Основна суть цього методу: замість x потрібно додати нову змінну таким чином, щоб отриманий в результаті інтеграл виявився простішим. 

Введемо нову змінну t: x=φ (t); dx=φ /(t) dt; t= φ-1(x). Продиференціюємо цей рядок і виразимо нову змінну через стару. Треба знайти межі змінних змінної t.

Тому знаходимо α як обернену функцію φ від а; β – як обернену функцію φ від b. Новий інтеграл буде мати межі від α до β, замість x – φ (t). Наступний крок полягає в обчисленні невизначеного інтеграла або первісної Φ від t. Далі повертаємося до змінної, яка була з самого початку, тобто до х: 

Φ= [φ-1(x)]+C. 

Якщо вам все-таки складно зрозуміти суть цього методу, краще звернутися до репетитора з математики. Допомога фахівця дозволить краще усвідомити всі математичні перетворення та без зайвих труднощів застосовувати інтеграли для розв’язання задач. 

Як виглядає метод інтегрування частинами?

Формула цього методу для визначеного інтеграла має наступний вигляд:

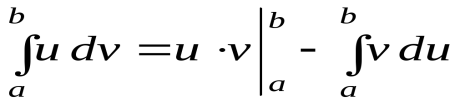Суть цієї формули: зробити у наступному інтегралі змінну v якомога простішою. 

Розглянемо її на простому прикладі: ʃ xsin xdx. У цьому інтегралі підінтегральною функцією виступає похідна лінійної функції х і тригонометричної функції sinх. Кожна з цих функцій окремо дуже добре інтегрується, але знайти похідну не так просто. 

Скористаємося методом: х=u, a sin xdx=dv. Тоді du=dx, v= –cosx. Підставимо отримані значення у формулу: ʃ xsin xdx= х(–cosx) – ʃ – cosx= – хcosx + sinx + C. 

Наочні приклади застосування інтегралів

Розглянемо приклад обчислення інтегралa за допомогою методу заміни змінних.

А ось випадок обчислення невизначеного інтеграла за допомогою методу інтегрування частинами: . Логарифм в підінтегральному виразі позначимо через u: , .

Тоді , . Перший множник містить логарифмічну функцію, а другий – ні:

Інтеграл починають вивчати в 11 класі. Це досить непроста тема, яка вимагає додаткового пояснення і тривалих занять. А займатися краще з репетитором. Заходьте на Букі, щоб знайти педагога відповідного рівня. Старша школа з Букі – це якісні матеріали для навчання, підготовки до ЗНО, онлайн курси та широкий вибір викладачів.